data_analysis
Data Analysis with Python
Python Tutorial
Applied Data Science Capstone
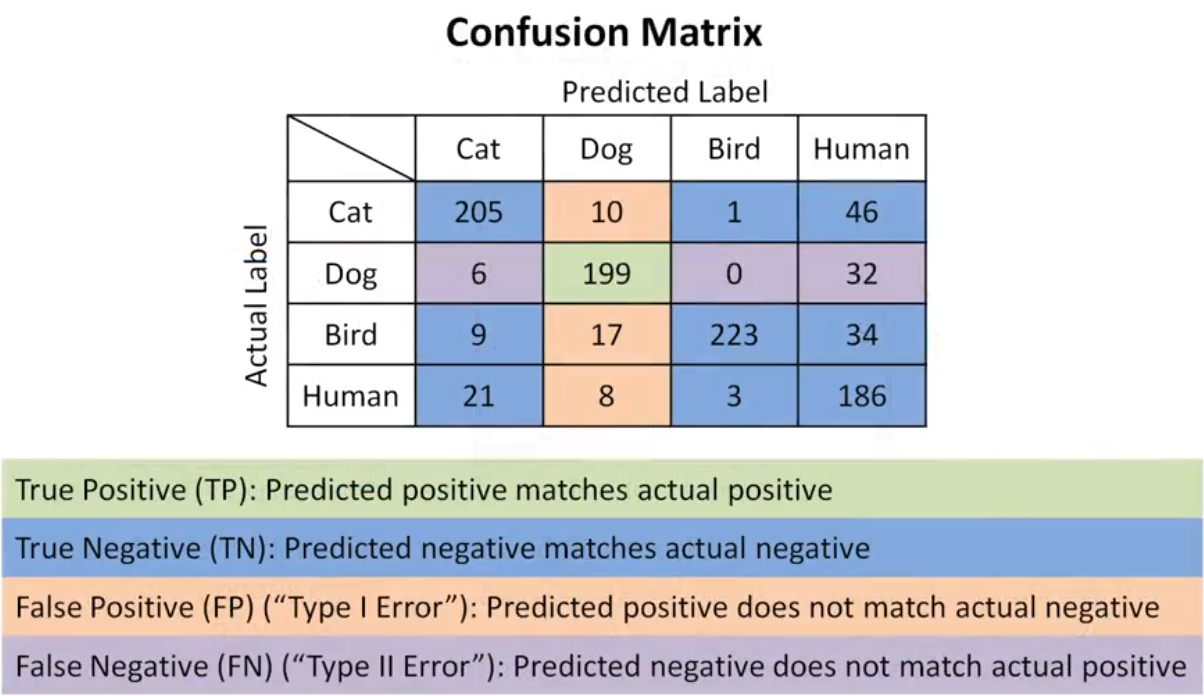
Confusion Matrix
- True Positive (TP) The actual value was positive, and the model predicted a positive value.
- True Negative (TN) The actual value was negative, and the model predicted a negative value.
- False Positive (FP) – Type I Error, The actual value was negative, but the model predicted a positive value.
- False Negative (FN) – Type II Error, The actual value was positive, but the model predicted a negative value.
ACCURACY = TP + TN / (TP + TN + FP + FN) F1 = 2TP/ (2TP + FP + FN)
library
| lib | Description |
|---|---|
| matplotlib | creating wide range of static, animated, and interactive visualizations |
| numpy | multidimensional array object for mathematical operations |
| pandas | working with “relational” or “labeled” data both easy and intuitive |
| scipy | high-level mathematical algorithms for statistical operations |
| seaborn | provides a high-level interface for drawing attractive and informative statistical graphics |
| folium | excellent for geospatial data visualization, also interactive & customizable |
| plotly | Highly interactive plots and dashboards, enable plotting in a web browser & wide range |
| pywaffle | Visualize proportional representation using squares or rectangles |
| scikit-learn | for machine learning and machine-learning-pipeline related functions |
pandas
Tabular data with heterogeneously-typed columns, as in an SQL table or Excel spreadsheet
Ordered and unordered (not necessarily fixed-frequency) time series data.
Arbitrary matrix data (homogeneously typed or heterogeneous) with row and column labels
Any other form of observational / statistical data sets. The data need not be labeled at all to be placed into a pandas data structure
pandas read/write data
| Data Formate | Read | Save |
|---|---|---|
| csv | pd.read_csv() |
df.to_csv() |
| json | pd.read_json() |
df.to_json() |
| excel | pd.read_excel() |
df.to_excel() |
| hdf | pd.read_hdf() |
df.to_hdf() |
| sql | pd.read_sql() |
df.to_sql() |
| ... | ... | ... |
Data acquisition
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
file_name = "/path/to/file"
df = pd.read_csv(file_name, header=0)
headers = ["symboling","normalized-losses","make","fuel-type","aspiration", "num-of-doors","body-style",
"drive-wheels","engine-location","wheel-base", "length","width","height","curb-weight","engine-type",
"num-of-cylinders", "engine-size","fuel-system","bore","stroke","compression-ratio","horsepower",
"peak-rpm","city-mpg","highway-mpg","price"]
# Assign appropriate header names to the data frame
df.columns = headers
# Replace the entries "?" with NaN entry from Numpy library
df = df.replace("?", np.nan)
# Retrieve the data types of the data frame columns
df.dtypes
# default use df.describe(include="all")
df[['length', 'compression-ratio']].describe()
# Retrieve the summary of the data set being used, from the data frame
df.info()
# simply drop whole row with NaN in "price" column
df.dropna(subset=["price"], axis=0, inplace=True)
# replace "?" to NaN
df.replace("?", np.nan, inplace = True)
missing_data = df.isnull()
missing_data.head(5)
# count missing data
for column in missing_data.columns.values.tolist():
print(column)
print (missing_data[column].value_counts())
print("")
# replace by mean
avg_norm_loss = df["normalized-losses"].astype("float").mean(axis=0)
df["normalized-losses"].replace(np.nan, avg_norm_loss, inplace=True)
# Convert data types to proper format
df[["bore", "stroke"]] = df[["bore", "stroke"]].astype("float")
df[["normalized-losses"]] = df[["normalized-losses"]].astype("int")
df[["price"]] = df[["price"]].astype("float")
df[["peak-rpm"]] = df[["peak-rpm"]].astype("float")
# Save the processed data frame to a CSV file with a specified path
df.to_csv("./file_updated.csv")
Data types
The main types stored in Pandas data frames are object, float, int, bool and datetime64. In order to better learn about each attribute, you should always know the data type of each column. In Pandas:
df.dtypes
# int64
Data Standarization
Standardization is the process of transforming data into a common format, allowing the researcher to make the meaningful comparison
MostFrequentEntry = df['attribute_name'].value_counts().idxmax()
df['attribute_name'].replace(np.nan,MostFrequentEntry)
df['attribute_name'].replace(np.nan,MostFrequentEntry, inplace=True)
AverageValue=df['attribute_name'].astype(<data_type>).mean(axis=0)
df['attribute_name'].replace(np.nan, AverageValue, inplace=True)
df[['attribute1_name', 'attribute2_name', ...]] = df[['attribute1_name', 'attribute2_name', ...]].astype('data_type')
# data_type is int, float, char, etc.
# data normalization
df['attribute_name'] = df['attribute_name']/df['attribute_name'].max()
# Binning is a process of transforming continuous numerical variables into discrete categorical 'bins' for grouped analysis.
bins = np.linspace(min(df['attribute_name']),
max(df['attribute_name'],n)
# n is the number of bins needed
GroupNames = ['Group1','Group2','Group3,...]
df['binned_attribute_name'] = pd.cut(df['attribute_name'], bins, labels=GroupNames, include_lowest=True)
# change column name
df.rename(columns={'old_name': 'new_name'}, inplace=True)
# An indicator variable (or dummy variable) is a numerical variable used to label categories. They are called 'dummies' because the numbers themselves don't have inherent meaning.
dummy_variable = pd.get_dummies(df['attribute_name'])
df = pd.concat([df, dummy_variable],axis = 1)
Correlation and Causation
Correlation: a measure of the extent of interdependence between variables.
Causation: the relationship between cause and effect between two variables.
It is important to know the difference between these two. Correlation does not imply causation. Determining correlation is much simpler the determining causation as causation may require independent experimentation.
Pearson Correlation
The Pearson Correlation measures the linear dependence between two variables X and Y.
The resulting coefficient is a value between -1 and 1 inclusive, where:
- 1: Perfect positive linear correlation.
- 0: No linear correlation, the two variables most likely do not affect each other.
- -1: Perfect negative linear correlation.
P-value
What is this P-value? The P-value is the probability value that the correlation between these two variables is statistically significant. Normally, we choose a significance level of 0.05, which means that we are 95% confident that the correlation between the variables is significant.
By convention, when the
- p-value is $<$ 0.001: we say there is strong evidence that the correlation is significant.
- the p-value is $<$ 0.05: there is moderate evidence that the correlation is significant.
- the p-value is $<$ 0.1: there is weak evidence that the correlation is significant.
- the p-value is $>$ 0.1: there is no evidence that the correlation is significant.
from scipy import stats
# Let's calculate the Pearson Correlation Coefficient and P-value of 'wheel-base' and 'price'.
pearson_coef, p_value = stats.pearsonr(df['wheel-base'], df['price'])
print("The Pearson Correlation Coefficient is", pearson_coef, " with a P-value of P =", p_value)
# output: The Pearson Correlation Coefficient is 0.5846418222655085 with a P-value of P = 8.076488270732338e-20
# conclusion
# Since the p-value is 0.001, the correlation between wheel-base and price is statistically significant, although the linear relationship isn't extremely strong (~0.585).
# Horsepower vs. Price
pearson_coef, p_value = stats.pearsonr(df['horsepower'], df['price'])
print("The Pearson Correlation Coefficient is", pearson_coef, " with a P-value of P = ", p_value)
# output: The Pearson Correlation Coefficient is 0.8095745670036559 with a P-value of P = 6.36905742825956e-48
# conclusion
# Since the p-value is 0.001, the correlation between horsepower and price is statistically significant, and the linear relationship is quite strong (~0.809, close to 1).
# Value counts is a good way of understanding how many units of each characteristic/variable we have.
df['drive-wheels'].value_counts()
# We can convert the series to a dataframe as follows:
df['drive-wheels'].value_counts().to_frame()
# The "groupby" method groups data by different categories
df['drive-wheels'].unique()
# calculate the average price for each of the different categories of data
df_group_one = df[['drive-wheels','body-style','price']]
df_grouped = df_group_one.groupby(['drive-wheels'], as_index=False).agg({'price': 'mean'})
df_gptest = df[['drive-wheels','body-style','price']]
grouped_test1 = df_gptest.groupby(['drive-wheels','body-style'],as_index=False).mean()
# A pivot table is like an Excel spreadsheet, with one variable along the column and another along the row.
grouped_pivot = grouped_test1.pivot(index='drive-wheels',columns='body-style')
grouped_pivot = grouped_pivot.fillna(0) #fill missing values with 0
# Let's use a heat map to visualize the relationship between Body Style vs Price.
plt.pcolor(grouped_pivot, cmap='RdBu')
plt.colorbar()
plt.show()
# regression plot
# Engine size as potential predictor variable of price
sns.regplot(x="engine-size", y="price", data=df)
plt.ylim(0,)
df[["engine-size", "price"]].corr()
# weak linear relationship
sns.regplot(x="peak-rpm", y="price", data=df)
df[['peak-rpm','price']].corr()
# A good way to visualize categorical variables is by using boxplots.
sns.boxplot(x="body-style", y="price", data=df)
""" Residual Plot
A residual plot is used to display the quality of polynomial regression. This function will regress y on x as
a polynomial regression and then draw a scatterplot of the residuals.
Residuals are the differences between the observed values of the dependent variable and the predicted values
obtained from the regression model. In other words, a residual is a measure of how much a regression line vertically
misses a data point, meaning how far off the predictions are from the actual data points.
"""
sns.residplot(data=df,x='header_1', y='header_2')
sns.residplot(x=df['highway-mpg'], y=df['price'])
""" KDE
A Kernel Density Estimate (KDE) plot is a graph that creates a probability distribution curve for the data based
upon its likelihood of occurrence on a specific value. This is created for a single vector of information. It is
used in the course in order to compare the likely curves of the actual data with that of the predicted data.
"""
sns.kdeplot(X)
""" Distribution Plot
This plot has the capacity to combine the histogram and the KDE plots. This plot creates the distribution curve
using the bins of the histogram as a reference for estimation. You can optionally keep or discard the histogram
from being displayed. In the context of the course, this plot can be used interchangeably with the KDE plot.
"""
sns.distplot(X,hist=False)
Data modeling
Simple Linear Regression
$$ Yhat = a + b X $$
- a refers to the intercept of the regression line, in other words: the value of Y when X is 0
- b refers to the slope of the regression line, in other words: the value with which Y changes when X increases by 1 unit
Multiple Linear Regression
$$ Yhat = a + b_1 X_1 + b_2 X_2 + b_3 X_3 + b_4 X_4 $$ $$ a: intercept\\\ b_1 :coefficients \ of\ Variable \ 1\ b_2: coefficients \ of\ Variable \ 2\ b_3: coefficients \ of\ Variable \ 3\ b_4: coefficients \ of\ Variable \ 4\ $$
Polynomial regression is a particular case of the general linear regression model or multiple linear regression models.
We get non-linear relationships by squaring or setting higher-order terms of the predictor variables.
There are different orders of polynomial regression:
$$ Yhat = a + b_1 X +b_2 X2 $$
$$ Yhat = a + b_1 X +b_2 X2 +b_3 X3\\\ $$
$$ Y = a + b_1 X +b_2 X2 +b_3 X3 ....\ $$
Simple Linear Regression Model (SLR) vs Multiple Linear Regression Model (MLR)
Usually, the more variables you have, the better your model is at predicting, but this is not always true. Sometimes you may not have enough data, you may run into numerical problems, or many of the variables may not be useful and even act as noise. As a result, you should always check the MSE and R^2.
In order to compare the results of the MLR vs SLR models, we look at a combination of both the R-squared and MSE to make the best conclusion about the fit of the model.
- MSE: The MSE of SLR is 3.16x10^7 while MLR has an MSE of 1.2 x10^7. The MSE of MLR is much smaller.
- R-squared: In this case, we can also see that there is a big difference between the R-squared of the SLR and the R-squared of the MLR. The R-squared for the SLR (~0.497) is very small compared to the R-squared for the MLR (~0.809).
This R-squared in combination with the MSE show that MLR seems like the better model fit in this case compared to SLR.
Simple Linear Model (SLR) vs. Polynomial Fit
- MSE: We can see that Polynomial Fit brought down the MSE, since this MSE is smaller than the one from the SLR.
- R-squared: The R-squared for the Polynomial Fit is larger than the R-squared for the SLR, so the Polynomial Fit also brought up the R-squared quite a bit.
Since the Polynomial Fit resulted in a lower MSE and a higher R-squared, we can conclude that this was a better fit model than the simple linear regression for predicting "price" with "highway-mpg" as a predictor variable.
Multiple Linear Regression (MLR) vs. Polynomial Fit
- MSE: The MSE for the MLR is smaller than the MSE for the Polynomial Fit.
- R-squared: The R-squared for the MLR is also much larger than for the Polynomial Fit.
Linear regression refers to using one independent variable to make a prediction.
You can use multiple linear regression to explain the relationship between one continuous target y variable and two or more predictor x variables.
Simple linear regression, or SLR, is a method used to understand the relationship between two variables, the predictor independent variable x and the target dependent variable y.
When using residual plots for model evaluation, residuals should ideally have zero mean, appear evenly distributed around the x-axis, and have consistent variance. If these conditions are not met, consider adjusting your model.
Use distribution plots for models with multiple features: Learn to construct distribution plots to compare predicted and actual values, particularly when your model includes more than one independent variable. Know that this can offer deeper insights into the accuracy of your model across different ranges of values.
The order of the polynomials affects the fit of the model to your data. Apply Python's polyfit function to develop polynomial regression models that suit your specific dataset.
To prepare your data for more accurate modeling, use feature transformation techniques, particularly using the preprocessing library in scikit-learn, transform your data using polynomial features, and use the modules like
StandardScalerto normalize the data.Pipelines allow you to simplify how you perform transformations and predictions sequentially, and you can use pipelines in scikit-learn to streamline your modeling process.
To determine the fit of your model, you can perform sample evaluations by using the Mean Square Error (MSE), using Python’s
mean_squared_errorfunction from scikit-learn, and using the score method to obtain the R-squared value.A model with a high R-squared value close to 1 and a low MSE is generally a good fit, whereas a model with a low R-squared and a high MSE may not be useful
Be alert to situations where your R-squared value might be negative, which can indicate overfitting.
When evaluating models, use visualization and numerical measures and compare different models.
The mean square error is perhaps the most intuitive numerical measure for determining whether a model is good.
A distribution plot is a suitable method for multiple linear regression.
An acceptable r-squared value depends on what you are studying and your use case.
To evaluate your model’s fit, apply visualization, methods like regression and residual plots, and numerical measures such as the model's coefficients for sensibility:
Use Mean Square Error (MSE) to measure the average of the squares of the errors between actual and predicted values and examine R-squared to understand the proportion of the variance in the dependent variable that is predictable from the independent variables.
When analyzing residual plots, residuals should be randomly distributed around zero for a good model. In contrast, a residual plot curve or inaccuracies in certain ranges suggest non-linear behavior or the need for more data.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import StandardScaler, PolynomialFeatures
from sklearn.pipeline import Pipeline
from sklearn.metrics import mean_squared_error, r2_score
import warnings
warnings.filterwarnings("ignore", category=UserWarning)
%matplotlib inline
file_name = 'laptop_pricing_dataset_mod3.csv'
df = pd.read_csv(file_name, header=0)
df.head()
# Single Linear Regression
lm = LinearRegression()
X = df[['CPU_frequency']]
Y = df['Price']
lm.fit(X,Y)
Yhat=lm.predict(X)
ax1 = sns.distplot(df['Price'], hist=False, color="r", label="Actual Value")
sns.distplot(Yhat, hist=False, color="b", label="Fitted Values" , ax=ax1)
plt.title('Actual vs Fitted Values for Price')
plt.xlabel('Price')
plt.ylabel('Proportion of laptops')
plt.legend(['Actual Value', 'Predicted Value'])
plt.show()
# Evaluate the Mean Squared Error and R^2 score values for the model
mse_slr = mean_squared_error(df['Price'], Yhat)
r2_score_slr = lm.score(X, Y)
print('The R-square for Linear Regression is: ', r2_score_slr)
print('The mean square error of price and predicted value is: ', mse_slr)
# Multiple Linear Regression
lm1 = LinearRegression()
Z = df[['CPU_frequency','RAM_GB','Storage_GB_SSD','CPU_core','OS','GPU','Category']]
lm1.fit(Z,Y)
Y_hat = lm1.predict(Z)
# Plot the Distribution graph of the predicted values as well as the Actual values
ax1 = sns.distplot(df['Price'], hist=False, color="r", label="Actual Value")
sns.distplot(Y_hat, hist=False, color="b", label="Fitted Values" , ax=ax1)
plt.title('Actual vs Fitted Values for Price')
plt.xlabel('Price')
plt.ylabel('Proportion of laptops')
mse_slr = mean_squared_error(df['Price'], Yhat)
r2_score_mlr = lm1.score(Z, Y)
print('The R-square for Multi Linear Regression is: ', r2_score_mlr)
print('The mean square error of price and predicted value is: ', mse_slr)
# Polynomial Regression
X = X.to_numpy().flatten()
f1 = np.polyfit(X, Y, 1)
p1 = np.poly1d(f1)
f3 = np.polyfit(X, Y, 3)
p3 = np.poly1d(f3)
f5 = np.polyfit(X, Y, 5)
p5 = np.poly1d(f5)
def PlotPolly(model, independent_variable, dependent_variabble, Name):
x_new = np.linspace(independent_variable.min(),independent_variable.max(),100)
y_new = model(x_new)
plt.plot(independent_variable, dependent_variabble, '.', x_new, y_new, '-')
plt.title(f'Polynomial Fit for Price ~ {Name}')
ax = plt.gca()
ax.set_facecolor((0.898, 0.898, 0.898))
fig = plt.gcf()
plt.xlabel(Name)
plt.ylabel('Price of laptops')
PlotPolly(p1, X, Y, 'CPU_frequency')
PlotPolly(p3, X, Y, 'CPU_frequency')
PlotPolly(p5, X, Y, 'CPU_frequency')
r_squared_1 = r2_score(Y, p1(X))
print('The R-square value for 1st degree polynomial is: ', r_squared_1)
print('The MSE value for 1st degree polynomial is: ', mean_squared_error(Y,p1(X)))
r_squared_3 = r2_score(Y, p3(X))
print('The R-square value for 3rd degree polynomial is: ', r_squared_3)
print('The MSE value for 3rd degree polynomial is: ', mean_squared_error(Y,p3(X)))
r_squared_5 = r2_score(Y, p5(X))
print('The R-square value for 5th degree polynomial is: ', r_squared_5)
print('The MSE value for 5th degree polynomial is: ', mean_squared_error(Y,p5(X)))
# Pipeline
# Create a pipeline that performs parameter scaling, Polynomial Feature generation and Linear regression
Input=[('scale',StandardScaler()), ('polynomial', PolynomialFeatures(include_bias=False)), ('model',LinearRegression())]
pipe=Pipeline(Input)
Z = Z.astype(float)
pipe.fit(Z,Y)
ypipe=pipe.predict(Z)
print('MSE for multi-variable polynomial pipeline is: ', mean_squared_error(Y, ypipe))
print('R^2 for multi-variable polynomial pipeline is: ', r2_score(Y, ypipe))
Model Evaluation
from tqdm import tqdm
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
from sklearn.model_selection import train_test_split, cross_val_score, GridSearchCV
from sklearn.linear_model import LinearRegression, Ridge
from sklearn.preprocessing import PolynomialFeatures
file_name = "laptops.csv"
df = pd.read_csv(file_name, header=0)
df.head()
df.drop(['Unnamed: 0', 'Unnamed: 0.1'], axis=1, inplace=True)
df.head()
# Divide the dataset into x_data and y_data parameters
y_data = df['Price']
x_data=df.drop('Price',axis=1)
# Split the data set into training and testing subests
x_train, x_test, y_train, y_test = train_test_split(x_data, y_data, test_size=0.10, random_state=1)
print("number of test samples :", x_test.shape[0])
# number of test samples : 24
print("number of training samples:",x_train.shape[0])
# number of training samples: 214
# Create a single variable linear regression model
lre=LinearRegression()
lre.fit(x_train[['CPU_frequency']], y_train)
print(lre.score(x_test[['CPU_frequency']], y_test))
# -0.06599437350393766
print(lre.score(x_train[['CPU_frequency']], y_train))
# 0.14829792099817962
# Run a 4-fold cross validation on the model and print the mean value of R^2 score along with its standard deviation.
Rcross = cross_val_score(lre, x_data[['CPU_frequency']], y_data, cv=4)
print("The mean of the folds are", Rcross.mean(), "and the standard deviation is" , Rcross.std())
# The mean of the folds are -0.1610923238859522 and the standard deviation is 0.38495797866647274
# Overfitting
x_train, x_test, y_train, y_test = train_test_split(x_data, y_data, test_size=0.5, random_state=0)
lre = LinearRegression()
Rsqu_test = []
order = [1, 2, 3, 4, 5]
for n in order:
pr = PolynomialFeatures(degree=n)
x_train_pr = pr.fit_transform(x_train[['CPU_frequency']])
x_test_pr = pr.fit_transform(x_test[['CPU_frequency']])
lre.fit(x_train_pr, y_train)
Rsqu_test.append(lre.score(x_test_pr, y_test))
plt.plot(order, Rsqu_test)
plt.xlabel('order')
plt.ylabel('R^2')
plt.title('R^2 Using Test Data')
# Ridge Regression (prevents overfitting)
pr=PolynomialFeatures(degree=2)
x_train_pr=pr.fit_transform(x_train[['CPU_frequency', 'RAM_GB', 'Storage_GB_SSD', 'CPU_core', 'OS', 'GPU', 'Category']])
x_test_pr=pr.fit_transform(x_test[['CPU_frequency', 'RAM_GB', 'Storage_GB_SSD', 'CPU_core', 'OS', 'GPU', 'Category']])
Rsqu_test = []
Rsqu_train = []
Alpha = np.arange(0.001,1,0.001)
pbar = tqdm(Alpha)
for alpha in pbar:
RigeModel = Ridge(alpha=alpha)
RigeModel.fit(x_train_pr, y_train)
test_score, train_score = RigeModel.score(x_test_pr, y_test), RigeModel.score(x_train_pr, y_train)
pbar.set_postfix({"Test Score": test_score, "Train Score": train_score})
Rsqu_test.append(test_score)
Rsqu_train.append(train_score)
plt.figure(figsize=(10, 6))
plt.plot(Alpha, Rsqu_test, label='validation data')
plt.plot(Alpha, Rsqu_train, 'r', label='training Data')
plt.xlabel('alpha')
plt.ylabel('R^2')
plt.ylim(0, 1)
plt.legend()
# Grid search
parameters1= [{'alpha': [0.0001,0.001,0.01, 0.1, 1, 10]}]
RR=Ridge()
Grid1 = GridSearchCV(RR, parameters1,cv=4)
Grid1.fit(x_train[['CPU_frequency', 'RAM_GB', 'Storage_GB_SSD', 'CPU_core', 'OS', 'GPU', 'Category']], y_train)
BestRR=Grid1.best_estimator_
print(BestRR.score(x_test[['CPU_frequency', 'RAM_GB', 'Storage_GB_SSD', 'CPU_core','OS','GPU','Category']], y_test))
# 0.3009905048691819
Classifier
# Pandas is a software library written for the Python programming language for data manipulation and analysis.
import pandas as pd
# NumPy is a library for the Python programming language, adding support for large, multi-dimensional arrays and matrices, along with a large collection of high-level mathematical functions to operate on these arrays
import numpy as np
# Matplotlib is a plotting library for python and pyplot gives us a MatLab like plotting framework. We will use this in our plotter function to plot data.
import matplotlib.pyplot as plt
#Seaborn is a Python data visualization library based on matplotlib. It provides a high-level interface for drawing attractive and informative statistical graphics
import seaborn as sns
# Preprocessing allows us to standarsize our data
from sklearn import preprocessing
# Allows us to split our data into training and testing data
from sklearn.model_selection import train_test_split
# Allows us to test parameters of classification algorithms and find the best one
from sklearn.model_selection import GridSearchCV
# Logistic Regression classification algorithm
from sklearn.linear_model import LogisticRegression
# Support Vector Machine classification algorithm
from sklearn.svm import SVC
# Decision Tree classification algorithm
from sklearn.tree import DecisionTreeClassifier
# K Nearest Neighbors classification algorithm
from sklearn.neighbors import KNeighborsClassifier
np.random.seed(0)
from js import fetch
import io
data = pd.read_csv('https://cf-courses-data.s3.us.cloud-object-storage.appdomain.cloud/IBM-DS0321EN-SkillsNetwork/datasets/dataset_part_2.csv')
X = pd.read_csv('https://cf-courses-data.s3.us.cloud-object-storage.appdomain.cloud/IBM-DS0321EN-SkillsNetwork/datasets/dataset_part_3.csv')
Y = data['Class'].to_numpy()
data.drop(['Class'], axis=1, inplace=True)
df = data._get_numeric_data()
transform = preprocessing.StandardScaler()
# fit the StandardScaler to the numerical columns in X
# numerical_columns = ['PayloadMass', 'Flights', 'Block', 'ReusedCount']
# X_scaled = preprocessing.StandardScaler().fit_transform(X[numerical_columns])
# Reassign the standardized data to X
# X = X_scaled
scaler = preprocessing.StandardScaler().fit(X)
X = scaler.transform(X)
X = transform.fit_transform(X)
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2, random_state=2)
print(X_train.shape, X_test.shape)
print(Y_train.shape, Y_test.shape)
# LogisticRegression
parameters ={"C":[0.01,0.1,1],'penalty':['l2'], 'solver':['lbfgs']}# l1 lasso l2 ridge
lr=LogisticRegression()
logreg_cv = GridSearchCV(lr, parameters, cv=10)
logreg_cv.fit(X_train, Y_train)
print("tuned hpyerparameters :(best parameters) ",logreg_cv.best_params_)
print("accuracy :",logreg_cv.best_score_)
# tuned hpyerparameters :(best parameters) {'C': 0.01, 'penalty': 'l2', 'solver': 'lbfgs'} accuracy : 0.8464285714285713
logreg_score = logreg_cv.score(X_test, Y_test)
def plot_confusion_matrix(y,y_predict):
"this function plots the confusion matrix"
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y, y_predict)
ax= plt.subplot()
sns.heatmap(cm, annot=True, ax = ax); #annot=True to annotate cells
ax.set_xlabel('Predicted labels')
ax.set_ylabel('True labels')
ax.set_title('Confusion Matrix');
ax.xaxis.set_ticklabels(['did not land', 'land']); ax.yaxis.set_ticklabels(['did not land', 'landed'])
plt.show()
yhat=logreg_cv.predict(X_test)
plot_confusion_matrix(Y_test,yhat)
# support vector machine
parameters = {'kernel':('linear', 'rbf','poly','rbf', 'sigmoid'),
'C': np.logspace(-3, 3, 5),
'gamma':np.logspace(-3, 3, 5)}
svm = SVC()
gscv = GridSearchCV(svm, parameters, scoring='accuracy', cv=10)
svm_cv = gscv.fit(X_train, Y_train)
print("tuned hpyerparameters :(best parameters) ",svm_cv.best_params_)
print("accuracy :",svm_cv.best_score_)
# tuned hpyerparameters :(best parameters) {'C': 1.0, 'gamma': 0.03162277660168379, 'kernel': 'sigmoid'} accuracy : 0.8482142857142856
svm_score = svm_cv.score(X_test, Y_test)
yhat=svm_cv.predict(X_test)
plot_confusion_matrix(Y_test,yhat)
# decision tree classifier
parameters = {'criterion': ['gini', 'entropy'],
'splitter': ['best', 'random'],
'max_depth': [2*n for n in range(1,10)],
'max_features': ['auto', 'sqrt'],
'min_samples_leaf': [1, 2, 4],
'min_samples_split': [2, 5, 10]}
tree = DecisionTreeClassifier()
trcv = GridSearchCV(tree, parameters, cv=10)
tree_cv = trcv.fit(X_train, Y_train)
print("tuned hpyerparameters :(best parameters) ",tree_cv.best_params_)
print("accuracy :",tree_cv.best_score_)
# tuned hpyerparameters :(best parameters) {'criterion': 'gini', 'max_depth': 2, 'max_features': 'sqrt', 'min_samples_leaf': 2, 'min_samples_split': 5, 'splitter': 'random'}
# accuracy : 0.875
tree_score = tree_cv.score(X_test, Y_test)
yhat = tree_cv.predict(X_test)
plot_confusion_matrix(Y_test,yhat)
# k nearest neighbors
parameters = {'n_neighbors': [1, 2, 3, 4, 5, 6, 7, 8, 9, 10],
'algorithm': ['auto', 'ball_tree', 'kd_tree', 'brute'],
'p': [1,2]}
KNN = KNeighborsClassifier()
knncv = GridSearchCV(KNN, parameters, cv=10)
knn_cv = knncv.fit(X_train, Y_train)
print("tuned hpyerparameters :(best parameters) ",knn_cv.best_params_)
print("accuracy :",knn_cv.best_score_)
# tuned hpyerparameters :(best parameters) {'algorithm': 'auto', 'n_neighbors': 10, 'p': 1}
# accuracy : 0.8482142857142858
knn_score = knn_cv.score(X_test, Y_test)
yhat = knn_cv.predict(X_test)
plot_confusion_matrix(Y_test,yhat)
df_score = pd.DataFrame({
'score': [logreg_score, svm_score, tree_score, knn_score]
}, index=['logreg', 'svm', 'tree', 'knn'])
df_score.plot(kind='bar', rot=45)
plt.xlabel('Model') # add to x-label to the plot
plt.ylabel('Score') # add y-label to the plot
plt.title('ML model score on Space launches') # add title to the plot
plt.show()
df_score.head()
# finds the best score
df_score.idxmax()
Page Source